

Instances of Axiom 1:
The first example asserts: if everything exemplifies the property P, then if a exists, then a exemplifies P. The second example says something similar. In formal terms, these examples tell us that we may instantiate the name a or variable z into a universal quantifier if we know that the constant a or the variable z denotes something. And we know both of these by axiom (45.2) above.
The third example asserts: if a exemplifies every property, then if P exists, then a exemplifies P. The fourth example says something similar. In formal terms, examples 3 and 4 tell us that we may instantiate names of, and variables for, properties into universal claims if we know that a simple property name or variable has a denotation. And we know that they do by axiom (45.2) above.
The fifth example asserts: if everything exemplifies P, then if the x that exemplifies Q exists, then the x that exemplifies Q exemplifies P. Intuitively, we may not instantiate a description into a universal claim unless we know that the description denotes something.
The sixth example asserts: if a exemplifies every property, then if being a y that bears R to the x that exemplifies Q exists, then a exemplifies being a y that bears R to the x that exemplifies Q. In this case, we know that the property being a y that bears R to the x that exemplifies Q exists, i.e., [λy Ry℩xQx]↓, by axiom (45.2), since the λ. doesn bind a variable in any encoding formula that is a subterm of the λ-expression.
In general, we may instantiate any term into a universal claim if we know that the term denotes something.Note that in all the examples, the term instantiated into the universal claim is substitutable for the variable. This is designed to avoid the situation in which a term gets `captured', when substituted into a quantified claim, by a quantifier for that variable that already exists in the claim. For example, suppose the following claim is true: for every x, there is a y such that y is not identical with x. The variable y already appears in this claim bound by a quantifier. Now suppose we could instantiate the quantifier ‘for every x’ in this claim to the variable y (variables are guaranteed to denote, so they can be instantiated into universal claims) by removing the quantifier from the claim and replacing y for x everywhere x appears. The resulting claim would be: there is a y such that y is not identical with y, which is clearly false. Therefore, we would have proven a falsehood from a truth. The problem with substituting the variable y in this claim is that it was `captured' by the quantifier ‘there is a y’ that was already part of the claim. This alters the significance of the resulting sentence upon substitution, and the restriction that terms be substitutable for the quantified variable avoids this situation.
Instances of Axiom 2:
[Examples were discussed in the examples of Axiom 1.]
Instances of Axiom 3:
The first example asserts: if, for every x, if a exemplifies P, then x exemplifies Q, then if Pa, then every x exemplifies Q. In formal terms, we can move a universal quantifier across the antecedent of a conditional if the variable bound by the quantifier is not free in the antecedent. The restriction that the antecedent of the conditional contain no free occurences of the quantified variable prevents us from deriving a falsehood from a truth. For example, it is logically true that: every x is such that if x exemplifies P then x exemplifies P. But if we could move the quantifier across this conditional, we could conclude: if x exemplifies P, then every x exemplifies P. This is not a logical truth. It is false in those domains in which not all the elements are in the extension of P; in such domains, the sentence would be false when something that exemplifies P is assigned to x, for then the antecedent is true and the conclusion, every x exemplifies P, is false.
Instances of Axiom 4:
[Exercise.]
Instances of Axiom 5(a):
The first example asserts: If the x that exemplifies Q exemplifies P, then the x that exemplifies Q exists. In formal terms, this tells us that if a definite description appears in a true atomic formula, then the description has a denotation. The second example asserts: if a exemplifies the property being a y such that y bears R to the x that exemplifies Q, then the property being a y such that y bears R to the x that exemplifies Q exists. In formal terms, this tells us that the complex predicate itself must have a denotation if it appears in a true atomic formula, even if it has a definite description as a component.
We leave examples of Axiom 5(b) as exercises.
The Rule of Generalization (GEN):
It is
important to mention that our logic of quantification is one in which
formulas with free variables are assertable. This simply means that
claims (logical axioms, logical theorems, non-logical axioms, and
non-logical theorems) may be asserted even if contain a free variable.
Given the derived metarule GEN, it is an immediate consequence that
the universal closures of these axioms and theorems are also theorems.
So, for example, the logical axiom for the logic of encoding is: if it
is possible that x encodes F, then it is necessary
that x encodes F (◊xF → □xF).
This is a formula in which the variables
x and F are free. By two applications of GEN, it
follows that: for any property F and for any object x,
if it is possible that x encodes F, then it is necessary
that x encodes F, i.e.,
∀F∀x(◊xF →
□xF). This universal generalization is, therefore, a
logical theorem.
Metarule/Derived Rule: Universal Elimination (∀E)
Let us justify the (.2) version of the rule, where τ meets the following two preconditions, namely, (a) it is a primitive constant, a variable, or a λ-expression in which the initial λ does not bind any variable in any encoding formula subterm, and (b) it is substitutable for α in φ:
1. ∀αφ Premise 2. ∀αφ → (τ↓ → φ[τ/α]) Instance, axiom (45.2), given the preconditions on τ 3. τ↓ → φ[τ/α] from 1, 2, by Rule MP 4. τ↓ instance, axiom (45.2), given the preconditions on τ 5. φ[τ/α] from 3, 4 by Rule MP 6. ∀αφ → φ[τ/α] from 1–5, by Rule CP (conditional proof)
This justifies the second version of Rule ∀E: (a) it is a finite sequence, line 1 is a premise, line 2 is the first axiom of quantificational logic, line 3 results from lines 1 and 2 by MP, line 4 is the second axiom of quantificational logic, line 5 results from lines 3 and 4 by MP, and line 6 follows from lines 1–5 by the metarule of conditional proof.
Metarule/Deriverd Rule of Universal Introduction (∀I)
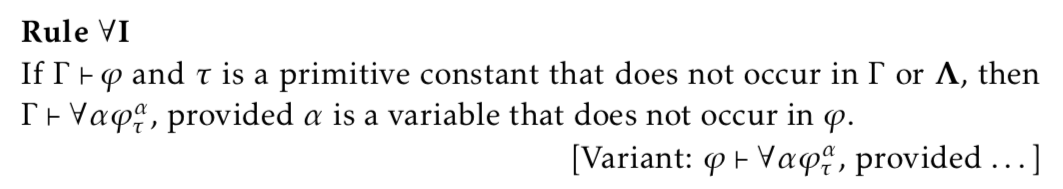
In this rule, Λ is the set of axioms of object theory, where these may be expressed using open formulas. So this rule can't be applied to universally generalize on a variable that occurs free in one of the axioms cited in the proof.
This is the classic principle by which we may derive a universal generalization by reasoning with respect to an arbitrarily chosen member of the domain, using only facts generally true of all the members of the domain, thus taking care not to import any special fact that is unique to the arbitrarily chosen member into the proof. Under such constraints, if we can show that the arbitrarily selected object has a property, then it follows that every member of the domain as that property. We shall not prove this rule but rather show it in action. Let us prove the following using UG:∀x(Px → Qx), ∀xPx ⊢ ∀xQxConsider the following sequence of formulas:
1. ∀x(Px → Qx) Premise 2. ∀xPx Premise 3. Pa → Qa from 1, by Rule ∀E, with a arbitrary 4. Pa from 2, by Rule ∀E 5. Qa from 3, 4, by Rule MP 6. ∀xQx from 5, by Rule ∀I
Notice that this constitutes a proof of everything exemplifies Q from everything that exemplifies P exemplifies Q and everything exemplifies P: it is a finite sequence, lines 1 and 2 are members of the premise set, lines 3 and 4 and results from lines 1 and 2, respectively, by a justified rule of inference, line 5 results from previous lines by MP, and line 6 results from line 5 by a justified rule. Notice also that in this proof, the constant symbol a did not occur in the premises and that the variable x does not occur in a exemplifies Q. So the Rule ∀I applies and we are entitled to conclude that everything exemplifies Q is derivable from the two given premises.
Fact: ⊢ ∀xPx → Px
This asserts that: it is a theorem that if everything exemplifies P, then x exemplifies P. Exercise: Demonstrate that this is true.
Fact: ⊢ ∀x(Px → Qx) → ∀x(¬Qx → ¬Px)
If we assume the rule of Contraposition from sentential logic, then we may demonstrate this fact as follows. Consider first the following sequence of formulas:
1. ∀x(Px → Qx) Premise 2. Pa → Qa from 1, by ∀E, with a arbitrary 3. ¬Qa → ¬Pa from 2, by contraposition 4. ∀x(¬Qx → ¬Px) from 3, by Universal Introduction (Rule ∀I) 5. ∀x(Px → Qx) → ∀x(¬Qx → ¬Px) from 1–4, by Conditional Proof
In this derivation, line 4 follows from lines 2 by the Rule of Contraposition. Given this derivation, notice that the conditions for applying the rule of Universal Generalization are met. So by UG, we know that there is a proof of “everything is such that if it doesn't exemplify Q it doesn't exemplify P” from “everything is such that if it exemplifies P then it exemplifies Q”. But by the Deduction Theorem, it follows that if we conditionalize the former on the latter, the result is a theorem of logic.