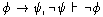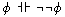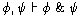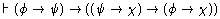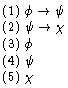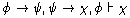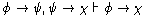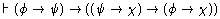Propositional Logic
Examples
The sentential logic of Principia Metaphysica is classical.
Although we have presented the logic axiomatically, our axiom system
has the same power as the `natural deduction' systems of sentential
logic that you find in any introductory text. These natural deduction
systems present the logic by describing introduction and elimination
rules for the connectives. These rules tell one how to draw
inferences to and from sentences involving these connectives within a
proof.
However, since we are using the axiomatic method rather than a
natural-deduction system, we first present the logic axiomatically and
then prove that the introduction and elimination rules used in
`natural deduction' systems are valid rules. The axiomatic
development of our sentential logic is presented in the item
Logic/Sentential Logic. For convenience, we reproduce the axioms and
rules of sentential logic here:
In what follows, we draw out consequences
and prove some facts about this logic.
Some Consequences:
In this section, we offer some basic examples of how to prove
consequences of the logical axioms using the rules of inference.
Basically, the method is to produce proof sequences. With this
method, all of the tautologies of sentential logic can be
derived as logical theorems.
Theorem of the Theory p:
This asserts that from the single premise
p we can derive the conditional if q then p. To see
that this claim is true, consider the following sequence of
formulas:This sequence constitutes a proof of
if q then p from the premise p because: (a) it
is a finite sequence of formulas ending in if q then p, (b)
the first member of the sequence is a member of the set of premises,
(c) the second member of the sequence is a logical axiom (this is an
instance of the first axiom schema of sentential logic), and (d) the
last member of the sequence follows from the first two by the rule
Modus Ponens. So all of the conditions for claiming that there is a
proof of if q then p from p are met.
Logical Theorem Schema:
This asserts that every instance of the
schema is a theorem of logic. To prove this, consider the following
sequence: This constitutes a proof of the
schema from the empty set of premises because: (a) it is finite
sequence of formulas ending with the schema, (b) line 1 is an instance
of the second axiom schema of sentential logic, (b) line 2 is an
instance of the first axiom schema of sentential logic, (c) line 3
follows from lines 1 and 2 by Modus Ponens, (d) line 4 is another
instance of the first axiom schema, and (3) line 5 follows from lines
3 and 4 by Modus Ponens. As a particular example, it follows that
if xF then xF is a theorem of logic.
Metatheorems and Derived Rules
In what follows, we describe and sometimes prove rules of inference
that can be derived from the basis of our logic. All of the natural
deduction rules can be derived, though we only sketch a few of these
rules.
Metatheorem (The Deduction Theorem) and Derived Rule
(Conditional Proof)
This claim constitutes a metatheorem about
the system of Principia Metaphysica. It embodies the derived
Rule of Conditional Proof. We shall not prove this metatheorem here,
but rather, offer an example. Assume as a premise that All Greeks
are European (let this be the sole element of the set of premises
designated by the Greek letter Gamma in the statement of the
metatheorem). Now consider the claim Clinton was Greek (let
this be the designation of the Greek letter phi). It is a fact that
by quantificational logic we can derive Clinton was European
from the premise and claim (let Clinton was European be the
designation of the Greek letter psi). And since Clinton was
Greek has no free variables, the conditions of the metatheorem
are met. So it tells us that from the premise All Greeks are
European alone, we can derive If Clinton was Greek, Clinton
was European. In what follows, when we prove a conditional (with
an antecedent having no free variables) by assuming the antecedent and
deriving the consequent, the justification for the proof is the Rule
of Conditional Proof (CP).
Derived Rule: Reductio Ad Absurdum (RAA)
To prove this is a good rule, we show that
any proof of phi from Gamma involving RAA can be converted to a proof
of phi from Gamma without using RAA. So suppose we have a proof of
phi from Gamma using RAA. Then, by assumption, the antecedent of the
rule is true. So if we apply the Deduction Theorem to the first
conjunct of the rule's hypothesis, we know: Call a sequence of formulas that must exist
according to this claim Sequence 1. Now if we apply the Deduction
Theorem to the second conjunct of the rule's antecedent, we know: Again, call the sequence of formulas that
must exist according to this claim Sequence 2. Now we produce a proof
of phi from Gamma without using RAA as follows: combine Sequence 1 and
Sequence 2; then append to this new sequence the third axiom of
sentential logic (in "Logic/Sentential Logic"):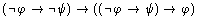 
;
now we append to the resulting sequence the
result of applying Modus Ponens to the axiom just added and the last
line of Sequence 1; finally we append to the resulting sequence the
result of applying Modus Ponens to the last line and the
last line of Sequence 2. The result constitutes a proof of phi from
Gamma without using RAA.
Derived Rule: Modus Tollens
Instead of a proof, we offer an example:
from the claims If the sun is shining, then John is happy and
It is not the case that John is happy, it follows by Modus
Tollens that It is not the case that the sun is shining. As
a more specific example involving the language of the theory, it
follows from the claims If it is possible that xF, then it is
necessary that xF and It is not necessary that xF that
It is not possible that xF.
Derived Rules: Double Negation
For example, from the claim John is
happy it follows by Double Negation that It is not the case
that it is not the case that John is happy, and vice versa. As a
more specifc example involving the language of the theory, it follows
from the claim that xF that It is not the case that it is
not the case xF, and vice versa.
Derived Rule: & Introduction
For example, from the premises John is
happy and Mary is sad we may draw the conjunctive
conclusion John is happy & Mary is sad. Similarly, from
aF and it is not the case that Fa, we may conclude
aF & it is not the case that Fa.
Exercise: Find an introductory logic text and
search for other rules of inference. Construct examples of these
rules. Find rules for & Elimination, Disjunction Introduction and
Elimination, Biconditional Introduction and Elimination,
Contraposition and Disjunctive Syllogism.
Some Further Theorems
We conclude with some examples that show the usefulness of the
rules of Conditional Proof and RAA.
Logical Theorem Schema:
To prove this Theorem Schema, first
consider the following sequence of formulas: Notice that this sequence of formulas
demonstrates the following fact: The sequence demonstrates this fact
because: (a) it is finite in length, (b) lines 1, 2, and 3 are all
premises, and (c) lines 4 and 5 follow from previous lines by Modus
Ponens. So, given this fact, it follows by the Deduction Theorem
that: And given two further applications of the
Deduction Theorem, we have proved:
Exercise:Prove the Law of Excluded Middle and
the Law of Noncontradiction using RAA.
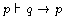
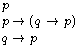
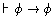
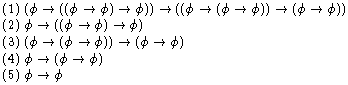
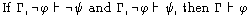
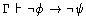
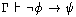
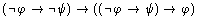