Basic Concepts in Modal Logic
Philosophy 169
Spring 1990
Syllabus
Professor:
Edward N. Zalta, Philosophy Department
Offices: Cordura 226 (CSLI) and 92EE (Philosophy)
Phone: 723-0345 (Cordura), 723-2192 (92EE)
Electronic Mail: zalta@csli
Mailboxes: Building 90 Lounge and Ventura Hall
Office Hours: At Cordura: Wednesday, 3 - 4:30, and by appointment
Class Meetings:
Lectures: Tuesday, Thursday, 1:15 - 2:30 P.M., Esmb (Mitchell) 138
Weekly `working' section, depending on class size and TA
availability
Course Description:
In this class we examine the structural similarities
among (the models of) various modal logics. It is customary in
philosophy to call the following propositional operators `modalities':
it is metaphysically necessary (possible) that, it is
physically necessary that, it is known (believed) by person S
that, it will be (was) the case that, it ought to be the
case that, and after every (some) terminating execution of the
program 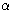 ,
it is the case that. These operators are called
`modalities' because when they are appled to a proposition p,
the proposition that results, for example, it is necessary that
p, expresses some way or mode in which p is true. So
modal logic is the study of the valid patterns of reasoning with
respect to each modality and why it is that the rules of inference
that legitimize such patterns never allow us to infer (modal)
falsehoods from (modal) truths. We shall see how these `logics' of
modality have been unified in a rather interesting way.
,
it is the case that. These operators are called
`modalities' because when they are appled to a proposition p,
the proposition that results, for example, it is necessary that
p, expresses some way or mode in which p is true. So
modal logic is the study of the valid patterns of reasoning with
respect to each modality and why it is that the rules of inference
that legitimize such patterns never allow us to infer (modal)
falsehoods from (modal) truths. We shall see how these `logics' of
modality have been unified in a rather interesting way.
Required Texts:
- Modal
Logic, by Brian Chellas
- Course Notes, handed out in class for a small xeroxing fee
Resource Texts:
- An Introduction to Modal Logic, George Hughes and Max
Cresswell
- A Companion to Modal Logic, George Hughes and Max
Cresswell
- Logics of Time and Computation, Robert Goldblatt
Course Prerequisite:
Philosophy 159 - You will have better perspective on things in
general if you have had 160A, but with 4 units worth of effort,
students with a 159 background should be able to come to a reasonably
deep understanding of the material.
Class Requirements
- 5 Problem Sets. As a group, the problem sets are worth
45%of your grade.
- MIDTERM EXAM (May 1): The midterm is worth 25%of your grade.
- FINAL EXAM (June 12): The final is worth 30%of your grade.
COURSE SCHEDULE
NOTE: The pace at which the material will be presented will
depend on the background of the students. Consequently, the following
schedule is tentative and subject to change. Reading assignments, and
exercise assignments, will be announced in class.
April
-
- 3 - Introduction to Modality
-
- 5 - A Modal Language
-
- 10 - Models for the Language
-
- 12 - Other Valid and Invalid Formulas
EXERCISES DUE
-
- 17 - Validity with respect to a Class of Models
-
- 19 - Preserving Validity and Truth; Rules of Inference
-
- 24 - Modal Logics and Theoremhood
EXERCISES DUE
-
- 26 - Deducibility, Consistent Sets and Maximal
Consistent Sets
May
-
- 1 - MIDTERM
-
- 3 - Normal Modal Logics
-
- 8 - Normal Logics and Maximal Consistent Sets
-
- 10 - Soundness of Modal Systems
EXERCISES DUE
-
- 15 - Canonical Models
-
- 17 - Completeness of Modal Systems
-
- 22 - Modal Predicate Logic: Language and Kripke Models
EXERCISES DUE
-
- 24 - Barcan Formulas
-
- 29 - Formulas Invalid in Kripke's Systems
-
- 31 - Other Applications of Modal Logic
June
-
- 5 - Dead Week
EXERCISES DUE
DATES OF THE EXAMS
1. Midterm: May 1
2. Final: Tuesday evening, June 12, 7:00 - 10:00 PM
GRADING POLICIES
1. Exercises are due at the beginning of class on the day
they are assigned as due. Exercise sets turned in after that time are
counted as late, and will be assessed, roughly, a 25%per diem
penalty (if you suppose that 100 points can be earned in the course,
and that each exercise set is therefore worth 9 points, then the
penalty for a late exercise is two points per day).
2. No make-up exams or incompletes will be given, unless
there is a genuine emergency or the circumstances are exceptional in
some other way.
3. Reevaluations: Students may request a reevaluation of an
exercise or exam problem if they feel that it has been incorrectly
graded. The work must be resubmitted to the professor within one week
of the date the problem was graded and returned.
Copyright © 1994, by Edward N. Zalta. All rights reserved.
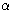 ,
it is the case that. These operators are called
`modalities' because when they are appled to a proposition p,
the proposition that results, for example, it is necessary that
p, expresses some way or mode in which p is true. So
modal logic is the study of the valid patterns of reasoning with
respect to each modality and why it is that the rules of inference
that legitimize such patterns never allow us to infer (modal)
falsehoods from (modal) truths. We shall see how these `logics' of
modality have been unified in a rather interesting way.
,
it is the case that. These operators are called
`modalities' because when they are appled to a proposition p,
the proposition that results, for example, it is necessary that
p, expresses some way or mode in which p is true. So
modal logic is the study of the valid patterns of reasoning with
respect to each modality and why it is that the rules of inference
that legitimize such patterns never allow us to infer (modal)
falsehoods from (modal) truths. We shall see how these `logics' of
modality have been unified in a rather interesting way.