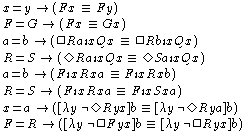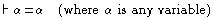The Logic of Identity
Examples
For convenience, we reproduce the following items from Principia
Metaphysica: Language/Object Identity, Language/Relation
Identity, and Logic/Logic of Identity: In this tutorial, we explain the definitions,
give some examples of the logical axiom, and then draw out some
consequences.
Explanation of the Definitions
The definition of object
identity tells us: objects x and y are identical if and only if
they are both ordinary objects and necessarily exemplify the same
properties or they are both abstract objects and necessarily encode
the same properties. Since every object is either ordinary or
abstract, and no object is both ordinary and abstract, we have a
completely general definition of object identity. Let us see how to
evaluate this definition. Consider President Clinton. In this world,
he didn't inhale when smoking marijuana. But he might have
inhaled---in some other possible world, Clinton did inhale. Of
course, we are considering a world where, by stipulation, it is
Clinton himself who inhaled the marijuana smoke. So we already know
that the Clinton in this alternative possible world (call him
`Clinton*') is identical with the Clinton of our world. But what is
it we know from a theoretical point of view when we know that Clinton
and Clinton* are the same object? Well, since they are both ordinary
objects, we know that they necessarily exemplify the same properties.
But this just amounts to the following: Clinton and Clinton* exemplify
the samme properties at w_1, Clinton and Clinton* exemplify
the same properties at w_2, Clinton and Clinton* exemplify
the same properties at w_3, and so on, for every possible world
w. This is perfectly consistent with the fact that Clinton
exemplifies the property not having inhaled in our world and fails
to exemplify this property in one of these other possible worlds,
for since Clinton and Clinton* are identical, these same facts
apply to Clinton*.
Similarly, abstract objects x and y are said to
be identical if and only if at every possible world, they encode the
same properties. Notice that this definition is consistent with the
existence of two distinct abstract objects which exemplify the same
properties.
Relation identity is defined in terms of the identity of
properties. Properties F and G are identical just
in case necessarily, they are encoded by the same objects. For
n > 1, n-place relations F and
G are identical iff for each way of plugging n - 1
objects in the same order into F and G, the
resulting 1-place properties are identical. For n = 0,
propositions p and q are identical if and only if
the properties being such that p and being such that
q are identical. It is important to remember that these
definitions do not tell us `how to find out' whether two apparently
distinct relations are in fact the same. Rather, they tell us what we
know from a theoretical point of view when we judge that two
apparently distinct relations are the same or in fact distinct. And
they tell us what we have to prove if we believe that, in some
theoretical context, we can prove that two relations are identical or
distinct.
Examples of the Logical Axiom
The single logical axiom governing our defined notions of identity
asserts basically two things: (a) if objects x and y are
identical, then any truth concerning x is a truth concerning y,
and (b) if n-place relations F and G are identical, any truth
concerning F is a truth concerning G. Here are some examples:
Careful consideration of these examples
reveals that there are no restrictions on the kinds of contexts in
which terms denoting identical objects or properties may be
substituted for one another. Of course, one cannot replace one term
by another in a situation where the second term is not substitutable
for the first. Even if we know that x = a, we may not
replace a by the variable x in the statement: b
exemplifies the property: being an x such that Rxa. Such a
substitution would alter the significance of the sentence. From the
fact that b exemplifies the property of being an x such
that x bears R to a, it does not follow that b
exemplifies the property of being an x such that x bears R to
x (at least, not unless we have the additional fact that a =
b).
Some Consequences:
Logical Theorems:
This tells us: (a) when x is
any object variable, it is a theorem that x = x, and (b) when
F is any n-place relation variable, it is a theorem
that F = F. To see that (a) is true, pick an arbitrary
object variable x. By the definition of ordinary
and abstract, we know that either O!x or
A!x. Suppose O!x. By the usual methods of proof,
we may derive the following theorem of sentential logic: Fx iff
Fx. So, by GEN, it is a theorem that: for every F, Fx iff
Fx. And by RN, it is a theorem that: Necessarily, for every
F, Fx iff Fx. So, given our supposition, we have proved that:
O!x & O!x & Necessarily, for every F, Fx iff Fx. So
by the definition of identity for objects (see the definition at the
top of this tutorial page), we have proved: x = x. But
suppose that A!x. Then, again, by the usual methods of
proof, we may derive the following logical theorem of sentential
logic: xF iff xF. So by GEN, it is a theorem that: for
every F, xF iff xF. So by RN, it is a theorem that:
Necessarily, for every F, xF iff xF. So, given our
assumption, we have proved: A!x & A!x & Necessarily, for
every F, xF iff xF. Thus, by the definition of identity for
objects, we have proved x = x. So by the rule of disjunctive
syllogism, we have established that x = x is a theorem.
To see that (b) is true, we argue by cases. First, pick an
arbitrary 1-place relation variable F. Then, by the
usual methods of proof for sentential logic, the following is a
theorem: xF iff xF. So by GEN, the following is a theorem:
for every x, xF iff xF. Now by RN, so is the following:
Necessarily, for every x, xF iff xF. So by the definition of
identity for 1-place relations (see the definition at the top
of this tutorial page), it follows that F = F. Second, pick
an arbitrary n-place relation variable F, for n
> 0. Exercise: Show that F = F. Third, pick an
arbitrary 0-place relation variable p. By our
reasoning in the first case, we already know that the following is a
theorem: the property being such that p = the property
being such that p. So, by the definition of identity for
0-place relations (see the definition at the top of this
tutorial page), the following is a theorem: p = p.
Logical Theorem:
derive x=x \rightarrow \Box x=x
derive alpha = alpha \rightarrow \Box alpha = alpha
Logical Theorem:
derive A!x and A!y and .... \rightarrow x=y
O!x O!y and .....\rightarrow x=y